La proporcionalidad es una relación entre magnitudes medibles. Es uno de los escasos conceptos matemáticos ampliamente difundido en la población. Esto se debe a que es en buena medida intuitiva y de uso muy común. La proporcionalidad directa es un caso particular de las variaciones lineales. El factor constante de proporcionalidad puede utilizarse para expresar las relaciones entre las magnitudes.
A) Proporción Directa
Dos cantidades a y b son Directamente Proporcionales si al aumentar o disminuir una de ellas, la otra aumenta o disminuye el mismo número de veces.
Se le simboliza como  ( k =cte. proporcionalidad)
( k =cte. proporcionalidad)
Los cuocientes que forman una
proporción directa tienen siempre un valor constante.
proporción directa tienen siempre un valor constante.
Su gráfica es una línea recta que pasa por el origen.
El símbolo matemático '∝' se utiliza para indicar que dos valores son proporcionales. Por ejemplo, A ∝ B.
En Unicode este es el símbolo: U+221D.
B) Proporción Inversa
Dos cantidades, a y b, son Inversamente Proporcionales cuando haciéndose mayor o menor la primera cantidad, la segunda se hace menor o mayor el mismo número de veces.
Se le simboliza como  (k = cte. proporcionalidad)
(k = cte. proporcionalidad)
El producto de dos cantidades inversamente proporcionales es siempre constante.
Su gráfica es asintótica al eje x.
C) Proporción Compuesta
Para resolver un problema de proporcionalidad compuesta debes seguir los
siguientes pasos:
1º.- Plantea la regla de tres. Expresa las cantidades de la misma magnitud en la
misma unidad.
2º.- Compara cada magnitud con la que lleva la x para ver si la proporcionalidad
entre ellas es directa o inversa. Escribe D debajo de las directas e I debajo de las
inversas.
3º.- Si hay alguna proporcionalidad inversa vuelve a plantear la regla de tres
invirtiendo las cantidades en las que sean inversas.
4º.- Escribe una proporción de la siguiente forma: la primera razón con las
cantidades de la magnitud donde está la x , la segunda razón con el producto de las
cantidades de las demás magnitudes.
Fíjate en el siguiente ejemplo.
Un taller, trabajando 8 horas diarias, ha necesitado 5 días para fabricar 1 000
piezas. ¿Cuántos días tardará en hacer 3 000 piezas trabajando 10 horas diarias?
Nºpiezas Horas día Días
1000 8 5
3000 10 x
(A doble de piezas, doble de días necesarios)
(A doble de horas diarias, mitad de días necesarios)
1000 10 5
3000 8 x
3000 . 8
1000 . 10
x
5
= 12
1000 . 10
5 . 3000 . 8
x = =
Tardará 12 días
Proporcionalidad mixta.
Un trozo de seda bordada de 12 m de largo y 5 de ancho cuesta 400 euros. ¿Qué trozo de
tela puedo comprar si necesito que sea de 4m de largo y dispongo de 200 euros? Se expresa el
enunciado en la siguiente tabla:
m largo m ancho €
12 5 400
4 ? 200
Se establecen las relaciones: A menor número de euros (e igual largo) menor altura de la tela, a
menor largo de tela mayor (e igual número de euros) mayor ancho de la tela.
Una vez extraídas las relaciones, se identifica la primera como relación de proporcionalidad directa y
la segunda de proporcionalidad inversa. Se procede a resolverlo por partes:
Si con 400 € puedo comprar un trozo de tela de 12 m de largo y 5m de alto, ¿qué alto podré comprar
con 200€ para el mismo largo?
400 € ⎯⎯→ 5 m alto (12 largo)
200 € ⎯⎯→ x m alto (12 largo) => x = 2
200 × 5
= 2,5 m (12 largo)
La segunda parte del problema es esta: Si con 200 € puedo comprar una tela de 12 m de largo y 2,5
de alto, ¿qué altura tendrá la tela si el largo es 4m?
12 m largo ⎯⎯→ 2,5 m alto (200€)
4 m largo ⎯⎯→ x m alto (200€)
=> x = 4
12 × 2,5
= 7,5 m alto, 4 m largo y 200€
PRIMER EJEMPLO
La receta de un pastel de vainilla indica que para cuatro personas se necesitan 200 g de harina, 150 g de mantequilla, cuatro huevos y 120 g de azúcar. ¿Cómo adaptar la receta para cinco personas? Según varios estudios, la mayoría de la gente calcularía las cantidades para una persona (dividiendo entre cuatro) y luego las multiplicaría por el número real de personas, cinco, otras solo le sumarían lo que a una persona le corresponde. Una minoría no siente la necesidad de pasar por las cantidades unitarias (es decir por persona) y multiplicaría los números de la receta por 5/4 = 1,25 (lo que equivale a añadir cinco huevos, 250 g de harina; 187,5 g de mantequilla y 150 g de azúcar) tendrá el mismo sabor que el otro, si el cocinero aficionado se muestra tan bueno como el chef que escribió la receta.
Se dice que la cantidad de cada ingrediente es proporcional al número de personas y se representa esta situación mediante una tabla de proporcionalidad: coeficiente k no nulo ( en el ejemplo) tal que
en el ejemplo) tal que
 en el ejemplo) tal que
en el ejemplo) tal que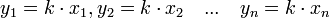
Si se consideran  e
e 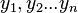 como valores de variables
como valores de variables  e
e 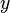 , entonces se dice que estas variables son proporcionales; la igualdad y = k·x significa que y es una Función lineal de x.
, entonces se dice que estas variables son proporcionales; la igualdad y = k·x significa que y es una Función lineal de x.
La representación gráfica de esta función es una recta que pasa por el origen del sistema de coordenadas. Una variación (incremento o decremento) de x da lugar a una variación proporcional de y (y recíprocamente, puesto que k≠0: y = 1/k · x):
 e
e 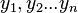 como valores de variables
como valores de variables  e
e 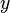 , entonces se dice que estas variables son proporcionales; la igualdad y = k·x significa que y es una Función lineal de x.
, entonces se dice que estas variables son proporcionales; la igualdad y = k·x significa que y es una Función lineal de x.La representación gráfica de esta función es una recta que pasa por el origen del sistema de coordenadas. Una variación (incremento o decremento) de x da lugar a una variación proporcional de y (y recíprocamente, puesto que k≠0: y = 1/k · x):

Son las funciones más sencillas que existen y las primeras que se estudian en clase dematemáticas, con alumnos de trece años aproximadamente.
La relación «Ser proporcional a» es
- reflexiva ( toda variable es proporcional a sí misma, con el coeficiente 1)
- simétrica (cuando y es proporcional a x entonces x lo es a y, con el coeficiente inverso) y
- transitiva (si x es proporcional a y, e y a z, entonces x lo es con z, multiplicando los coeficientes)
por lo que se trata de una relación de equivalencia. En particular dos variables proporcionales a una tercera serán proporcionales entre sí).
La tabla del primer ejemplo se puede descomponer en tres de formato dos por dos:
por tanto las propiedades de la proporcionalidad se ilustran preferentemente con tablas de cuatro casillas.
Una proporción está formada por los números a, b, c y d, si la razón entre a y b es la misma que entre c y d.
Una proporción está formada por dos razones iguales:
a : b = c : d
Dónde a, b, c y d son distintos de cero y se lee a es a b como c es a d .
Proporción múltiple:
Una serie de razones está formada por tres o más razones iguales:
a : b = c : d = e : f
Y se puede expresar como una proporción múltiple:
a : c : e = b : d : f
En la proporción hay cuatro términos; a y d se llaman extremos; c y b se llaman medios.
En toda proporción el producto de los extremos es igual al producto de los medios.
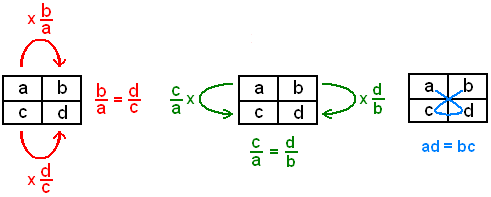
Para establecer que una tabla es proporcional, se puede:
- verificar que la segunda columna es múltiple de la primera, (primera tabla: para pasar de la primera casilla a la segunda, hay que multiplicar por
 ; en la segunda línea se tiene que multiplicar por
; en la segunda línea se tiene que multiplicar por  , luego estas fracciones deben ser iguales para obtener columnas proporcionales)
, luego estas fracciones deben ser iguales para obtener columnas proporcionales) - verificar que la segunda línea es múltiple de la primera (segunda tabla, con un raciocinio parecido) o
- verificar la igualdad de los productos cruzados: a·d = b·c. (tercera tabla: las igualdades anteriores equivalen a a·d = b·c, cuando no hay valores nulos, que por cierto no tienen un gran interés en este contexto). ya que no se puede comprobar.
Dos autos recorren exactamente el mismo camino. Al primero le ha tomado dos horas y media llegar al destino, rodando a una velocidad promedia de 70 km/h. El segundo rueda a 100 km/h. ¿Cuánto tiempo ha tardado en llegar?
Entre mayor velocidad tenga uno, menor tiempo durará el viaje. Si se multiplica por dos la velocidad, la duración del viaje se dividirá por dos. Aquí, claramente el tiempo del recorrido no es proporcional a la velocidad sino justamente lo contrario: es inversamente proporcional, es decir proporcional a la inversa de la velocidad. Esto permite responder a la pregunta:
cambiando una multiplicación por una división (primera tabla) o aplicando la proporcionalidad con la inversa de la velocidad (segunda tabla). El tiempo será  , es decir una hora y 45 minutos.
, es decir una hora y 45 minutos.
 , es decir una hora y 45 minutos.
, es decir una hora y 45 minutos.Más generalmente, si una variable y es inversamente proporcional a otra variable x, se puede aplicar la proporcionalidad con  , o más bien utilizar la siguiente equivalencia:
, o más bien utilizar la siguiente equivalencia:
 , o más bien utilizar la siguiente equivalencia:
, o más bien utilizar la siguiente equivalencia:Es decir que el producto de los valores correspondientes (aquí en la misma línea) es constante. En el ejemplo: 70 × 2,5 = 100 × 1, 75 = 175km, que es la longitud del recorrido.
Una tabla de variación proporcional es aquella que sigue una secuencia utilizando de base el precio de algún objeto u otra cosa que pueda aumentar o disminuir cierto número u objeto de forma proporcional. ejem:
número de canicas precio
- 2 canicas 50 centavos
- 4 canicas 1 peso
- 6 canicas 1,50 pesos
Magnitudes Directamente Proporcionales:
Dos magnitudes son directamente proporcionales cuando al multiplicar o dividir una de ellas por un número,la otra queda multiplicada o dividida respectivamente por el mismo número.
Ejemplo:
Un automóvil consume 3 galones de gasolina por 120 km de recorrido ¿Cuantos kilómetros recorre con 20 galones?
Observamos que las magnitudes son directas Si la razón o cociente entre ellas es un valor constante.Con los datos de la tabla, hallamos la razón.
Elaboramos una tabla de proporcionalidad:
Gasolina 3 1 10 20 40 (galones)
Recorrido 120 40 400 800 1600 (kilómetros)
Con 20 galones de gasolina, el auto recorre 800 kilómetros: Mientras más kilómetros se recorran, mas galones de gasolina de consumirán. El número de kilómetros recorridos es directamente proporcional (D.P) al número de galones de gasolina. Siempre que las demás condiciones se mantuvieran constantes. Esto es, que no se modificaran las condiciones climáticas o geográficas que modificaran el consumo.