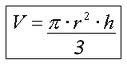FÓRMULAS PARA OBTENER EL VOLUMEN DEL CILINDRO Y DEL CONO
Veremos un tema de matemáticas de la rama de geometría, que implica la obtención del volumen de los cuerpos : cilindro y cono.
Como primer paso conoceremos las formulas para estos cuerpos:
La formula es:
Vcilindro= (Ab) (h)
Debido a que la labse del cilindro es un circulo utilizaremes la fórmula para obtener el área de un circulo y posteriormente se multiplica por la altura del cilindro:
A= (π)(2r)
Vcilindro= (π)(2r)(h)
La segunda formula es para obtener el volumen del cono, en donde se utliza d ebase la formula del cilindro.
Pero debido a que el cilindro al dividirse en partes proporcinales en forma conica nos da como resultado tres conos proporcionales; por tanto nuestra formula que de la siguiente manera:
Apliquemos lo aprednido en el siguiente ejemplo:
Ontener el volumen del cilindro
radio=5 cm.
altura=12cm.
2
Vcilindro= (π)(r2)(h)
Sustituimos Valores: tomando en cuenta π=3.14
Vcilindro= (3.14)(52cm.)(12cm.)
teniendo como resultado= 942 cm3
Hay que tener en cuenta que todo resultado consta de un valor numerico y de una magnitud en este caso centímetros los cuales al ser un cuerpo y estar buscando su volumen se extresa en centómetros cubicos.
Ahora practiquemos con la fromula del volumen dle cono:
radio= 4 cm.
altura= 10 cm.
Sustituimos valores:
v= (π)(r2)(h)/3
v= (3.14) (4cm2) (10cm.)/3
v=167.46 cm3
De esta manera hemos apredido las formulas para obtener el volumen de un curpo cilindrico y cónico.
Cabe mencionar que nuestro conocimiento se reforzará de acuerdo a la complejidad de los porblemas que s enos apliquen lo que nunca cambiara serán nuestras formulas para obtener el volumen del cilindro y del cono.
Normalista Especialidad Matemáticas: Leticia Mariana San Vicente Del Angel
