LA HISTORIA DE LOS NÚMEROS ENTEROS Y SU REPRESENTACIÓN GRÁFICA

  “El número reside en todo lo que es conocido. Sin él es imposible pensar nada ni conocer nada.”

Desde la era primitiva el hombre siempre buscó respuestas a sus inquietudes. La inquietud permitió la aparición de conceptos abstractos en la mente del hombre primitivo ya evolucionado. Cuando el hombre desarrolla la capacidad de darle sentido racional a las cosas, nace el concepto de cantidad.

La creación de los números naturales dependió no solo de un hombre en particular sino de la intervención de varios hombres para regularizar y hacer práctico su uso.

Los números naturales son aquellos que utilizamos para contra "uno" 1, "dos" 2, "tres" 3.... y utilizamos este nombre para diferenciarlo de  números fraccionarios: "1/5", "3/3" etc. para diferenciarlo de números decimales "2.5", "6.3" etc. los números enteros pueden ser tanto positivos como negativos.

Desde que nos levantamos a diario para realizar nuestras labores, utilizamos el número natural. Algunas veces  no nos percatamos de esto, pero basta con que pensemos en el número de días de una semana, o como futura docente podría pensar en el número de alumnos que atenderé.  Entonces, que los números naturales tiene dos primeras características: la cardinalidad y la ordinalidad.

La representación simbólica de los números naturales, se presupone que surgió antes del nacimiento de las palabras para “representarlos”, seguramente porque es más fácil contar muescas en un palo que establecer una frase para identificar un número concreto. Los símbolos que representan a los números no han sido siempre los mismos. Citamos a continuación la simbolización de diversas culturas respecto a los números naturales, según su contexto.

     

 

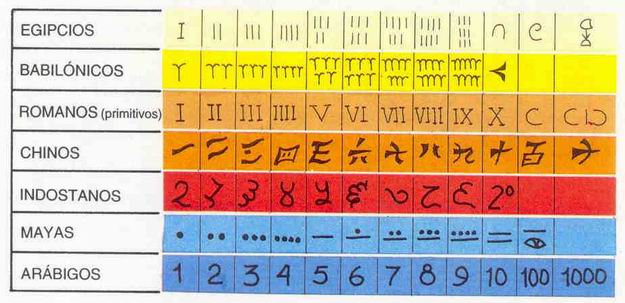
Finalmente se estableció el conjunto de los números naturales, con la notación adoptada por la letra N, y es el siguiente:

Ν = {0,1,2,3,4,...,100,101,....}

Se observa que los números están ordenados, entonces podemos relacionarlo con puntos mediante la recta numérica, cumpliendo una relación de punto a número, siendo así un ejemplo de la característica infinita de los naturales.

Estoy incluyendo el cero en los números naturales. Sin embargo según la Teoría de Números, el cero no debe incluirse en los números naturales. Los pitagóricos clasificaron los números (naturales) en pares e impares y, probablemente, la designación de números perfectos, que se encuentra en Euclides (Egipto Ptolemaico, alrededor de 365 d.C.-275 a.C.)7, para aquellos números como el 6, 28, 496, 8128 que tienen la propiedad de ser iguales a la suma de sus divisores menores que él; luego los números amigos para aquellos como 220 y 284, cada uno de los cuales es la suma de los divisores del otro.

Los números naturales se pueden sumar y multiplicar, pero no todos se pueden restar o dividir. Es por esto que se hace una extensión al conjunto de los naturales, la necesidad de completitud genera el conjunto de los números negativos.

Los números negativos

Los números negativos antiguamente conocidos como “números deudos” o “números absurdos”, datan de una época donde el interés central era la de convivir con los problemas cotidianos a la naturaleza.

Las primeras manifestaciones de su uso se remontan al siglo V, en oriente, y no llega hasta occidente hasta el siglo XVI. En oriente se manipulaban números positivos y negativos, estrictamente se utilizaba los ábacos, usando tabillas o bolas de diferente color.

Representación gráfica de los números enteros

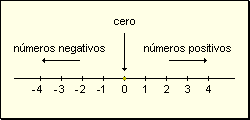
Los números enteros se representan gráficamente en una recta:

-Los números positivos se ubican a partir del punto 0 hacia la derecha.
-Los números negativos se ubican a partir del punto 0 hacia la izquierda.
-Si dos números son iguales, les corresponde el mismo punto en la recta numérica.
-Si un número es menor a otro, el menor se ubica a la izquierda del mayor.
-Si un número es mayor a otro, el mayor se ubica a la derecha del menor.
-Cada número y su opuesto están a igual distancia del cero.

 

El conjunto de números enteros se designa con la letra Z. A partir de su representación gráfica se observa que:

-El conjunto de números enteros no tiene ni primer ni último elemento.
-Todo número entero tiene un antecesor y un sucesor.
- Entre dos números enteros existe un número finito de números enteros, por lo que el conjunto es discreto.

Valor absoluto

Los números 3 y -3 tienen igual valor absoluto, ya que:

 A partir de esta definición podemos decir que:

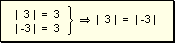
- Dos números enteros son iguales cuando tienen igual valor absoluto e igual signo.
- Dos números enteros son opuestos cuando tienen igual valor absoluto y distinto signo.

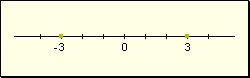
Relación de mayor

- Siendo dos números enteros positivos, un número entero a es mayor que otro b si el valor absoluto de a es mayor al valor absoluto de b.

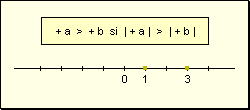
- Siendo números enteros negativos, un número entero a es mayor que otro b si el valor absoluto de a es menor al valor absoluto de b.

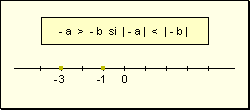
- Siendo dos números enteros de distinto signo, un número entero a es mayor que otro b si a es positivo.

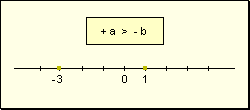
Relación de mayor

Análogamente:

- Siendo dos números enteros positivos, un número entero a es menor que otro b si el valor absoluto de a es menor al valor absoluto de b.

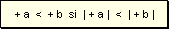
- Siendo números enteros negativos, un número entero a es menor que otro b si el valor absoluto de a es mayor al valor absoluto de b.

-Siendo dos números enteros de distinto signo, un número entero a es menor que otro b si a es negativo.

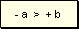
Conclusiones personales

1. Los números nacen junto la evolución del hombre, se origina de la práctica en la naturaleza.

2. La necesidad en la matemática la impulsa para ir cambiando y evolucionando.

3. Cada cultura dio manifestaciones de la noción de cantidad y la idea de número en sus representaciones.

4. Los enteros no fueron aceptados de manera universal hasta el siglo XVIII, sin embargo ya era usado por algunas culturas.

5. El cero no se origina formalmente junto con los números naturales.

6. Es necesario aplicar la historia de las matemáticas, como recurso didáctico, en el proceso de enseñanza y aprendizaje de las  matemáticas.

Es evidente la importancia que tienen los números enteros en nuestra vida y como futura docente en la especialidad de matemáticas la práctica de ellos será inevitable y aun que ya tenia conciencia  el gran valor que ejercen en mi vida personal y laboral la realización del presente ensayo me ayudo  atener más conocimiento acerca de el origen de estos números así como descifrar el por que  de las incógnitas que a veces se nos presentan como la  del cero.

Todo ese aprendizaje me será de gran apoyo para  explicar a mis futuros alumnos sobre la importancia que las matemáticas ejercen sobre nuestra vida, de esta forma ellos se sentirán con más entusiasmo para aprender de ella  pues los contenidos que les enseñaré solo será la teoría de la práctica que cotidianamente realiza en su vida logrando así el uso del verdadero aprendizaje significativo.